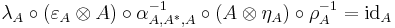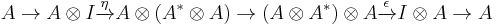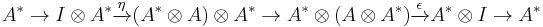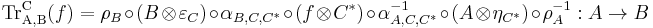Compact closed category

In category theory, compact closed categories are a general context for treating dual objects. The idea of a dual object generalizes the more familiar concept of the dual of a finite-dimensional vector space. So, the motivating example of a compact closed category is FdVect, the category with finite dimensional vector spaces as objects and linear maps as morphisms.

Contents

Definition

A symmetric monoidal category 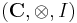(\mathbf{C},\otimes,I) is compact closed if every object 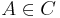A \in C has a dual object. If this holds, the dual object is unique up to canonical isomorphism, and it is denoted A^*.

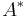In a bit more detail, an object 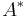A^* is called the dual of A if it is equipped with two morphisms called the unit 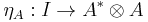\eta_A:I\to A^*\otimes A and the counit 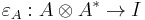\varepsilon_A:A\otimes A^*\to I, satisfying the equations

\lambda_A\circ(\varepsilon_A\otimes A)\circ\alpha_{A,A^*,A}^{-1}\circ(A\otimes\eta_A)\circ\rho_A^{-1}=\mathrm{id}_A

and

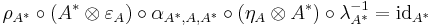\rho_{A^*}\circ(A^*\otimes\varepsilon_A)\circ\alpha_{A^*,A,A^*}\circ(\eta_A\otimes A^*)\circ\lambda_{A^*}^{-1}=\mathrm{id}_{A^*}.

For clarity, we rewrite the above compositions diagramatically:

A\to A\otimes I\xrightarrow{\eta}A\otimes (A^*\otimes A)\to (A\otimes A^*)\otimes A\xrightarrow{\epsilon} I\otimes A\to A

and

A^*\to I\otimes A^*\xrightarrow{\eta}(A^*\otimes A)\otimes A^*\to A^*\otimes (A\otimes A^*)\xrightarrow{\epsilon} A^*\otimes I\to A^*

Properties

Compact closed categories are a special case of monoidal closed categories, which in turn are a special case of closed categories.

Compact closed categories are precisely the symmetric autonomous categories. They are also *-autonomous.

Every compact closed category C admits a trace. Namely, for every morphism 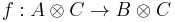f:A\otimes C\to B\otimes C, one can define

\mathrm{Tr_{A,B}^C}(f)=\rho_B\circ(B\otimes\varepsilon_C)\circ\alpha_{B,C,C^*}\circ(f\otimes C^*)\circ\alpha_{A,C,C^*}^{-1}\circ(A\otimes\eta_{C^*})\circ\rho_A^{-1}:A\to B

which can be shown to be a proper trace.

Examples

The canonical example is the category FdVect with finite dimensional vector spaces as objects and linear maps as morphisms. Here 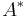A^* is the usual dual of the vector space A.

The category of finite-dimensional representations of any group is also compact closed.

The category Vect, with all vector spaces as objects and linear maps as morphisms, is not compact closed.

References

Kelly, G.M.; Laplaza, M.L. (1980). "Coherence for compact closed categories". Journal of Pure and Applied Algebra 19: 193–213. doi:10.1016/0022-4049(80)90101-2.